2.8. Signaux périodiques
Un signal
 se répéte à une période
se répéte à une période
 si :
si :

Pour tous
 . Un tel signal se répéterait aussi pour des périodes de
. Un tel signal se répéterait aussi pour des périodes de

En discutant des périodes des signaux audio numériques, nous nous apercevrons rapidement la difficulté pour décrire les signaux dont la "période" n'est pas un nombre entier, de sorte que l'équation ci-dessus n'est plus valable. Dans toute cette section, nous éviterons cette difficulté en supposant que le signal
 peut être interpolé avec les échantillons de sorte qu'il soit bien défini, que n soit un nombre entier ou pas.
peut être interpolé avec les échantillons de sorte qu'il soit bien défini, que n soit un nombre entier ou pas.
Un sinus à une période de
 ou
ou
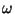 est la fréquence angulaire.
est la fréquence angulaire.
Plus généralement, toute somme de sinusoides avec des fréquences
 pour l'entier K, ont cette période, serie de Fourier :
pour l'entier K, ont cette période, serie de Fourier :

D'ailleurs, si nous définissons la notion d'interpolation assez soigneusement, nous pouvons représenter n'importe quel signal périodique comme une telle somme. Ceci est l'analyse discréte en fonction du temps de Fourier que vous verrez beaucoup par la suite.
Les fréquences angulaires des sinusoides ci-dessus, c.-à-d., les multiples de nombre entier de
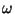 sont appelées les harmoniques de
sont appelées les harmoniques de
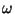 , qui est la fondamentale
, qui est la fondamentale
En terme de pitch les harmoniques ont un intervalle de 1200, 1902, 2400, 2786, 3102, 3369, 3600..., de cents par rapport à la fondamental. Cette séquence de pitch est quelquefois appellée serie harmonique.
les six premiers de ceci sont presque des multiples de 100 ; en d'autres termes, les six premiers harmoniques d'un pitch dans l'échelle occidentale sont près d'autres pitchs de la même échelle; le troisième (et le sixième) sont seulement à 2 cents et le cinquième à 14.
D'une autre manière, le rapport de fréquence 3:2 correspond presque à sept demi-ton, 4:3 correspond à peu prés à cinq demi-ton, et pour les rapports 5:4 et 6:5 quatre et trois demi-ton. Ces quatre intervalles s'appellent le cinquième, le quatrième et les tiers majeurs et mineurs.
Laissons les questions de phase de côté, nous pouvons utiliser une banque d'oscillateurs sinusoïdaux pour synthétiser des tonalités périodiques, en indiquant la fréquence fondamentale et les amplitudes (en fonction du temps).
La figure suivante montre comment faire. C'est un cas spécial de la synthèse additive ; plus généralement le terme peut être appliqué aux réseaux dans lesquels les fréquences des oscillateurs sont indépendamment contrôlables.
