Chapitre 2. Acoustique des signaux audio numériques
Le traitement acoustique numérique (analyse et/ou synthèse numérique sonore) est réalisé en traitant les signaux audio numériques. Ce sont des sequences de nombres,
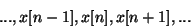
où l'index n, appelé nombre d'échantillon, peut être n'importe quels nombres entiers. Un nombre simple dans la sequence s'appelle un échantillon. (pour empêcher la confusion nous éviterons l'utilisation répandue et contradictoire du mot
Voici une sinusoïde réelle
représente l'amplitude,
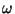est la fréquence angulaire, et
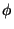la phase.
Pour le nombre d'échantillon
, la phase est égal à
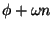
Nous parlons de sinusoïde réelle pour la distinguer de la sinusoïde complexe que nous verrons plus tard.
La figure suivante montre un sinus de 50 points, d'amplitude égal à 1, de fréquence angulaire égal à 0.24 et une phase égal à 0.
Les signaux sinusoïdaux joue un rôle majeur dans le traitement audio, car il est facile de calculer les effets de toutes les sortes d'opérations sur eux.
Les signaux audio numérique ne sont pas liés directement au temps, mais vous devez choisir un taux d'échantillonage, habituellement appelé
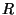qui est le nombre d'échantillon par seconde. Le temps est lié au nombre d'échantillon
ou
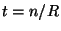
Un signal sinusoïdal avec la fréquence angulaire
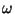a une fréquence en temps réel égale à
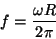
pour un cyle par seconde, car un cycle est égal à
radians et une seconde est égal à
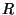échantillons.
L'amplitude d'un signal audio réel peut être exprimée comme une variation d'une pression atmosphérique ou d'une tension en fonction du temps, mais les échantillons d'un signal audio numérique sont des nombres réels (ou complexes comme vous le verrez dans les chapitres suivants).
Nous supposerons que les erreurs numériques approximatives sont négligeables, exactitude numérique, et que le format numérique permet aux échantillons de prendre n'importe quelle valeur, gamme illimitée.
Cependant, la plupart des matériels audio numérique fonctionnent seulement sur une gamme fixe de valeurs d'entrée et de sortie, fixons cette gamme de -1 à 1. Les logiciels de traitement audio numérique moderne emploient habituellement une représentation à virgule flottante pour les signaux, pour déterminer quelle est l'unité qui convient pour n'importe quelle tâche donnée, aussi longtemps que la sortie audio est dans la gamme du matériel.
2.1. Mesure de l'amplitude
À proprement parler, tous les échantillons d'un signal audio numérique sont des amplitudes, et nous pouvons parler de l'amplitude
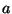du SINUSOID ci-dessus. Pour traiter les signaux audio numériques généraux, il est utile d'avoir les mesures d'amplitude.
L'amplitude et d'autres mesures sont la meilleure façon de savoir comment s'applique une fenêtre, une gamme fixe d' échantillons du signal.
Par exemple, la fenêtre commençant à l'échantillon
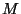de la longueur
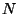d'un signal audio
comprend les échantillons,
Les deux mesures d'amplitude le plus fréquemment utilisées sont l'amplitude maximale (valeur crête), qui est simplement le plus grand échantillon (en valeur absolue) au-dessus de la fenêtre :
et la valeur RMS de l'amplitude :
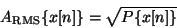
Px[n ] correspond à la puissance moyenne, définie comme :
Dans cette dernière formule, les signes de valeur absolue ne sont pas nécessaires tant que nous travaillons sur des signaux réels, mais nécessaire si les signaux complexe. L'amplitude crête et RMS de n'importe quel signal est au moins supérieur à zéro, et est seulement égal à zéro si le signal lui-même égal zéro.
L'amplitude RMS d'un signal peut égaler l'amplitude crête mais ne l'excède jamais; et elle peut être au minimum égal à
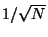fois la valeur crête.
Dans des conditions raisonnables (si la fenêtre contient au moins plusieurs périodes et si la fréquence angulaire est bien au-dessous de un radian par échantillon) l'amplitude maximale du SINUSOID est approximativement
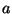et son amplitude RMS est
