2.2. Amplitude de signaux combinés
Si un signal
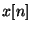 a une amplitude crête ou RMS
a une amplitude crête ou RMS
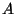 (dans une certaine fenêtre fixe) alors le signal mesuré
(dans une certaine fenêtre fixe) alors le signal mesuré
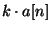 , ou
, ou
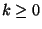 , a une amplitude
, a une amplitude
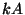
La puissance RMS du signal mesuré change par facteur de
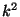
La situation devient plus compliquée quand deux signaux différents sont additionnés; connaitre les amplitudes des deux signaux ne suffit pas pour connaitre l'amplitude de la somme.
Les deux mesures d'amplitude obéissent au moins aux inégalités suivantes; pour deux signaux quelconques
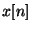 et
et
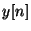
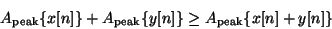
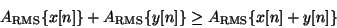
Si nous fixons une fenêtre de
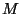 à
à
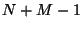 nous pouvons écrire la puissance moyenne de la somme de deux signaux comme :
nous pouvons écrire la puissance moyenne de la somme de deux signaux comme :
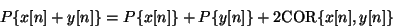
là nous avons introduit la corrélation de deux signaux :
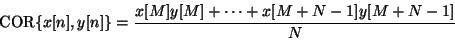
La corrélation peut être positive, égal à zéro, ou négative. Au-dessus d'une fenêtre suffisamment grande, la corrélation de deux sinusoides avec différentes fréquences est négligeable.
En général, pour deux signaux non-corrélatifs, la puissance de la somme est la somme des puissances :
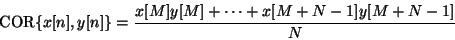
Pour l'amplitude, ceci devient :
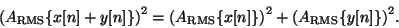
C'est le théoreme de pythagore. Des signaux non-corrélatifs peuvent être considérés comme des vecteurs perpendiculairement entre eux ; positivement corrélé en tant qu'ayant un angle aigu entre eux, et négativement corrélé en tant qu'ayant un angle obtus entre eux.
Par exemple, si nous avons deux signaux non-corrélatifs entre eux avec une amplitude RMS
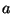 la somme aura l'amplitude RMS
la somme aura l'amplitude RMS
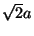 . D'autre part si les deux signaux s'avèrent être égaux (le plus corrélé possible) la somme aura l'amplitude
. D'autre part si les deux signaux s'avèrent être égaux (le plus corrélé possible) la somme aura l'amplitude
 qui est le maximum permis
qui est le maximum permis